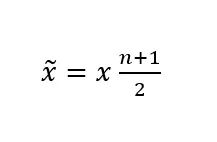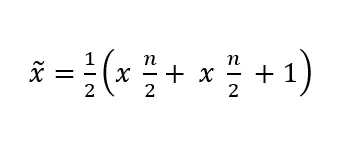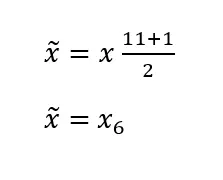Calcolare la mediana
In statistica ha senso raccogliere grandi quantità di dati solo se questi possono poi essere elaborati e analizzati. Il calcolo della mediana è un passaggio importante di questo processo. Tramite il calcolo della mediana è possibile ridurre un insieme di dati a una o poche cifre, cosicché relazioni complesse o temi specifici possano essere presentati in modo chiaro sotto forma di tabelle e diagrammi. Spiegheremo qui di seguito come calcolare e interpretare la mediana, passo dopo passo.
Che cos’è la mediana?
La mediana – detta anche valore centrale – viene dalla statistica e, data una lista di valori in ordine di grandezza, indica il valore che si trova esattamente a metà della stessa. Nella statistica descrittiva, la mediana è detta anche indice di posizione e viene utilizzata per esprimere la tendenza centrale di una raccolta dati.
Non confondere la mediana con il valore medio o la media. Questa si calcola facendo la somma di tutti i valori, dividendola poi per il numero totale di valori presenti. La mediana rappresenta, invece, il valore che si trova al centro di una lista di valori messi in ordine crescente.
Che formula si usa per calcolare la mediana?
Per calcolare la mediana di una serie di dati si possono usare due diverse formule, a seconda del numero di valori osservati. Il simbolo generale per la mediana è (cioè la lettera x con la tilde), dove indica il numero di valori osservati e rappresenta un valore specifico nella serie di dati.
Se il numero totale di valori osservati è dispari, utilizzate questa formula:
Vi spiegheremo qui di seguito entrambi i casi con due semplici esempi.
Calcolare la mediana: come fare
Esempio 1: numero dispari di valori
Nel nostro primo esempio abbiamo un numero dispari di valori osservati. Immaginate che a undici partecipanti a un seminario di formazione venga chiesta l’età e che le risposte siano le seguenti:
28, 34, 51, 19, 62, 43, 29, 38, 45, 26, 49
Il primo passo è di mettere le risposte in ordine crescente:
19, 26, 28, 29, 34, 38, 43, 45, 49, 51, 62
Ognuno dei valori dati corrisponde a un determinato valore . Cioè 19 = , 26 = , 28 = , ecc. Il vantaggio di un numero dispari di valori osservati è che adesso possiamo individuare subito la mediana. Nel nostro caso è = 38 perché questo valore divide la serie di numeri a metà. Metà delle età (19, 26, 28, 29, 34) è minore della mediana, mentre l’altra metà (43, 45, 49, 51, 62) è maggiore.
Potete anche calcolare la mediana applicando la formula della sezione precedente. sta per il numero di valori osservati, in questo caso 11. La formula è la seguente:
Dato che sta per 38, arriviamo allo stesso risultato. La mediana delle età raccolte al seminario è 38, poiché questo valore si trova esattamente a metà della lista dei numeri disposti in ordine di grandezza.
Esempio 2: numero pari di valori
In questo caso la mediana non è così facile da individuare perché il numero di valori osservati è pari e la mediana non è in una posizione centrale della serie di dati.
Immaginate che al seminario di formazione successivo si aggiunga un altro partecipante e che, questa volta, l’età venga quindi chiesta a dodici persone. Le risposte sono le seguenti:
28, 34, 51, 19, 62, 43, 29, 38, 45, 26, 49, 33
Adesso dovete riorganizzare i dati in ordine crescente, denominandoli da a .
19, 26, 28, 29, 33, 34, 38, 43, 45, 49, 51, 62
Con = 12 si utilizza la formula per i valori osservati pari:
La medianadelle età di questo secondo seminario è di 36 anni.
Se si lavora con il programma di fogli di calcolo Excel, non è necessario calcolare la mediana manualmente. Excel offre un’utile funzione mediana, che calcola il risultato corretto, rapidamente e senza errori.
Differenze rispetto alla media aritmetica e alla moda
Come abbiamo già spiegato, la mediana non deve essere confusa con il valore medio o la media, detta anche media aritmetica, che si usa per trovare il valore medio di un insieme di dati. Nel nostro primo esempio, l’età media sarebbe 38,5 (la somma dei dati divisa per il numero di partecipanti). Esiste poi anche la cosiddetta moda, che indica, invece, il valore più frequente in un set di dati. Nei nostri esempi, di fatto, tutti i valori sono una moda perché sono unici e nessuno di essi si ripete.
Utilizzo della mediana
Ma quando conviene calcolare la mediana e quando, invece, utilizzare la media aritmetica o la moda?
Dipende tutto dalla situazione. Anche se la media aritmetica è generalmente considerata più precisa e molto efficiente in statistica, è anche più sensibile agli outlier. Ciò significa che basta anche un solo dato sbagliato nella raccolta per distorcere il valore medio in modo considerevole. Anche se la mediana non è precisa o efficiente quanto la media aritmetica, è considerata più robusta e viene quindi spesso utilizzata quando i set di dati sono contaminati.
La moda, invece, si usa quando non si ha a che fare con valori numerici ma con altre caratteristiche, ad esempio se offrite un prodotto in diversi colori e volete scoprire quale colore viene acquistato più spesso.